cryptosystem.org

Let's say you've got a 2D image (or matrix) of the Laplacian of some function, and you want to solve for the function. This is actually relatively easy to do with MATLAB, but searching for a step-by-step example I came up with nothing, so I thought I'd show how to do it here.

Poisson's equation relates the Laplacian (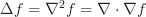 $\Delta f = \nabla^2 f = \nabla \cdot \nabla f$ ) of some function with its result:

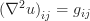
$\left(\nabla^2 u \right)_{ij}=g_{ij}$

So in the discrete Poisson equation we have 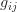$g_{ij}$ defined as the non-boundary subset of a 2-D rectangular matrix of dimensions 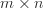$m \times n$ . Here 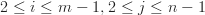$2 \le i \le m-1, 2 \le j \le n-1$ to allow for boundary conditions.

Transforming 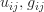$u_{ij}, g_{ij}$ into natural ordered vectors $\left[U\right], \left[b\right]$ allows us to rewrite as the 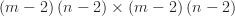$\left(m-2\right)\left(n-2\right) \times \left(m-2\right)\left(n-2\right)$ linear system:

$\left[A\right]\left[U\right] = \left[b\right]$

So, on to the juicy bit, how to express and solve this in MATLAB given you have a 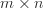$m \times n$ 2-D matrix defining 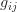$g_{ij}$ (for consistency, we'll use variable names equivalent to what's in these equations).

First, we need to reshape 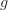$g$ into a 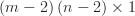$\left(m-2\right)\left(n-2\right)\times 1$ vector 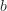$b$ that skips the boundaries:

b = -reshape(g(2:(m-1),2:(n-1)),(m-2)*(n-2),1);

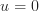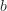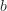If we have uniform Dirichlet boundary conditions $u=0$ , $b$ should now be correct. If you want other boundary conditions for $u$ , you'll need to add them to the appropriate positions in $b$ , which I won't cover here.

Thankfully, MATLAB has a nice built-in gallery of matrices which includes the sparse tridiagonal matrix we need for 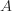$A$ :

A = gallery('poisson',m-2);

We can now solve using the backslash operator:

U = A\b;

This gives us the result in vector form which we can reshape back to what we want:

u = reshape(U,m-2,n-2);

You can pad back your 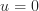$u = 0$ boundary conditions with:

u = padarray(u,[1 1]);

And verify the results with:

laplacian = del2(u)*4;

Which should correspond to 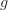$g$ (with, of course, border discrepancies). There is, perhaps, some entirely built-in way of doing all this, hidden somewhere in the terse documentation.